学校で習う電気の勉強って意外と覚えにくかったりしますよね。
電圧・電流・電力の関係性、オームの法則とか。
水とか火とか植物は目に見えるから、なんとなくイメージしやすい。
でも電気を目で見ることは難しいから、イメージつかない人が多いのかも?
ということで、電気の例えとして優秀なものがないか探してみようと思います。
よく例えがちな「水」からやってみよう!
※イメージしやすくするため、厳密には定義が異なる内容を含みます。
オームの法則のおさらい
まずオームの法則についておさらいです。
オームの法則
電圧 = 電流 x 抵抗
“ V = I x R ” なんて書き方もしますが、自分はそういうの苦手だったので、
できるだけ日本語で書いていきます。
” 電圧 = 電流 x 抵抗 “この式が成立するということは、
” 電流 = 電圧 ÷ 抵抗 “と
” 抵抗 = 電圧 ÷ 電流 “も成立します。
電圧・電流・抵抗のいずれか2つが分かれば、残りの一つも簡単に出てくるということですね。
掛け算の記号” x “は省略できるため、
V = IR
と覚えているとカッコイイです。
それぞれの要素にイメージを持ってみる
どんなことも、自分の中でイメージできることで格段に覚えやすくなります。
この記憶へとつながるキーワードがたくさんあるほど、この記憶を見つけやすいんです。
電圧
電圧はV(ボルト)で表す、電気の強さを示す数値です。
乾電池やモバイルバッテリー、コンセントなどが電圧と関わりの深い存在です。
例:「PKC!10万ボルトだ!」「1000万ボルト、ヴァーリー!」「高圧注意!(この圧は電圧の圧)」
電流
電流はA(アンペア)で表す、電気の流れる量を示す数値です。
冷蔵庫のコードや充電ケーブル、街中の電線が関わりの深いものになります。
例:「ブレーカー・30Aまで」「過電流対策品」
あんまりないかも… たこ足配線による事故は電流が関係しています。
抵抗
抵抗はΩ(オーム)で表す、電気の流れにくさを示す数値です。
電球やヒーターなどの電気を流すと熱くなるものが、抵抗と関わり深いイメージです。
例:「抵抗するな!」「それなら俺らも抵抗するで」
身の回りで電気に関係したものはたくさんありますが、関係してはいるものの、しっかりと目に見えたりしないですよね。
そのため、電気は水に置き換えて表現されがちです。
本題:水に置き換えて考えてみる
早速、電圧・電流・抵抗を上手いこと水に置き換えられないか考えてみました。
できることなら、
電圧→水圧 電流→水流 抵抗→水に与える抵抗
と、いきたいところですが、実際考えてみるとなんとなく腑に落ちない。
考え方はわかっても、身の回りに存在しない謎の道具が必要になったりします。
電圧・電流・電力の関係性の場合は問題ないんですけどね…
一度、各要素をイメージするため、条件を挙げてみましょう。
電圧に欲しい条件
- 一度決めたら基本的に変動しないこと。
- 大きいほど強いこと。
回路の問題や日常生活において、電圧はあまり変動せず、一定で考えるのが楽です。
大きいほど強いイメージは、持っておいて損はないと思います。
電流に欲しい条件
- 抵抗の数値が大きくなると小さく、小さくすると大きくなること。
- 物としての量を感じられること。
「電気が流れる」で電流ですから、流れるもののイメージを付けられると良さそうです。
抵抗に欲しい条件
- 数値を大きくすると電流が小さく、小さくすると電流が大きくなること。
- 流れを阻むイメージ
言葉のままの意味で、抵抗は電気の流れに抗う機能を持っています。
日常的に目にするもので例えてみる
普段の生活で見たことがあるものであり、水に関わるもので例えてみます。
色々と考えましたが、おそらくこれが丁度良いかもしれません。
電圧 → 蛇口
電流 → 水の流れる速さ
抵抗 → フィルター
結局、フィルター(抵抗)は普段の生活であまり見ないかもしれませんね。
味のある絵にしてみました。
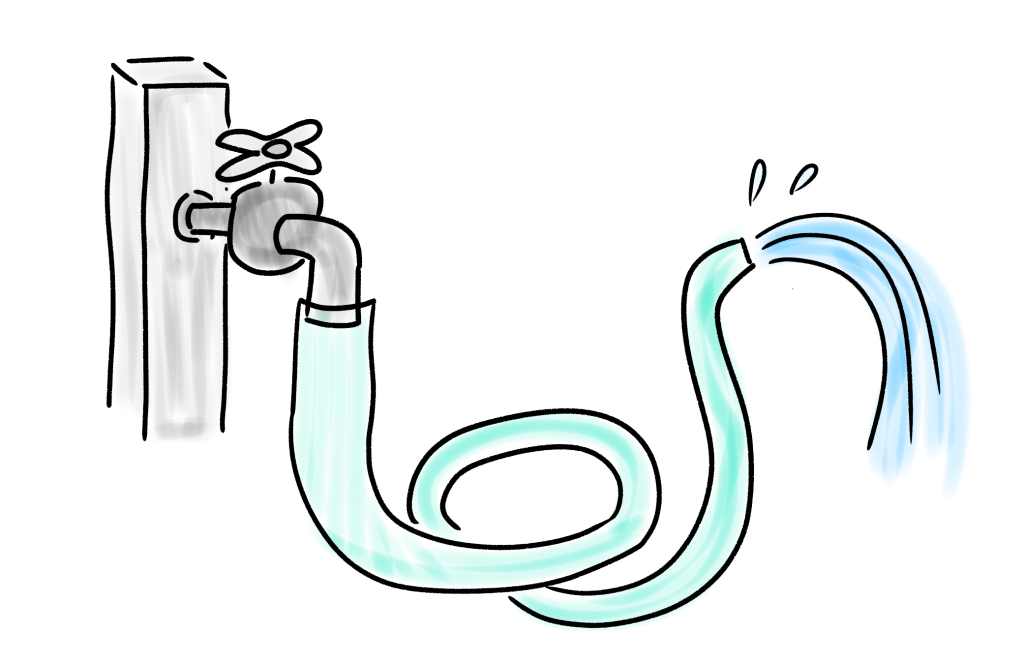
蛇口とホースとそこから出てくる水を描きました。
蛇口をどのくらいひねるか → 電圧 (蛇口からの水の量 → 電圧)
ホースから水が出てくる勢い → 電流 です。
ここに抵抗の概念を追加します。
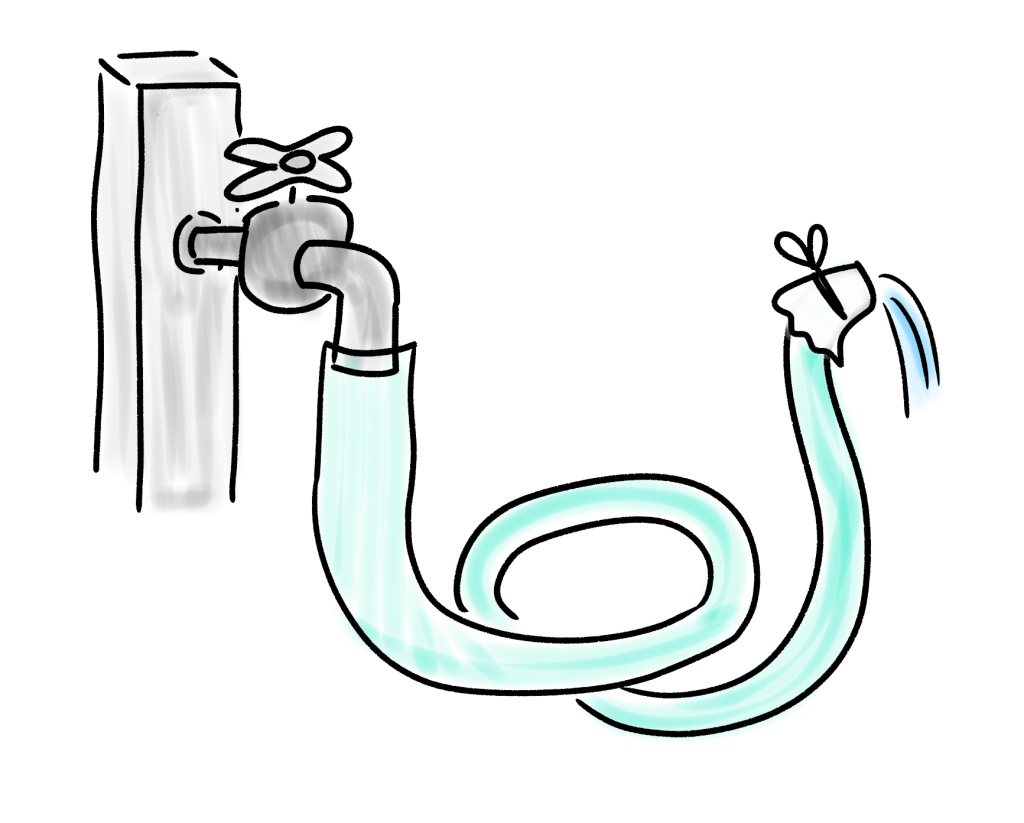
はい。ホース先端に布を当て、縛りつけました。
これがフィルター(抵抗)です。
関係性はこのような感じになっています。

この絵が成り立つのか、説明していきます。
置き換えた図で想像・公式化
オームの法則の登場人物を、蛇口・水の勢い・フィルターで表現してみました。
彼らがどのような動きをするか、頭の中で想像してみましょう。

1.まず蛇口をひねります。するとホースの先から水が出てきました。
2.ホースの先にフィルターを取り付けました。すると水の勢いが落ちました。
3.フィルターを2重にしてみました。さらに水の勢いが落ちました。
4.蛇口をさらにひねりました。水の勢いが増しました。
ここまでの動きは想像できましたか?
ここでしっかり想像してほしい内容はこちらです。
水の動きは蛇口から始まり、水がでてくる出口とフィルター位置で終わる
蛇口があり、ホースを通ってフィルターのある出口へ。これを式にすると…
蛇口 = 出口 x フィルター
つまり
電圧 = 電流 x 抵抗
xなのか÷なのかは若干あいまいですが、出口とフィルターの掛け合わせということで、
xでお願いします。
水の勢い = 出口 であるのは、水の勢いを見るためには出口から水が出てくる必要があるからですね。
この動きを基本に、電気の問題に当てはめてみましょう。
ひとまず電気の問題に当てはめてみる
簡単な問題に当てはめてみましょう。
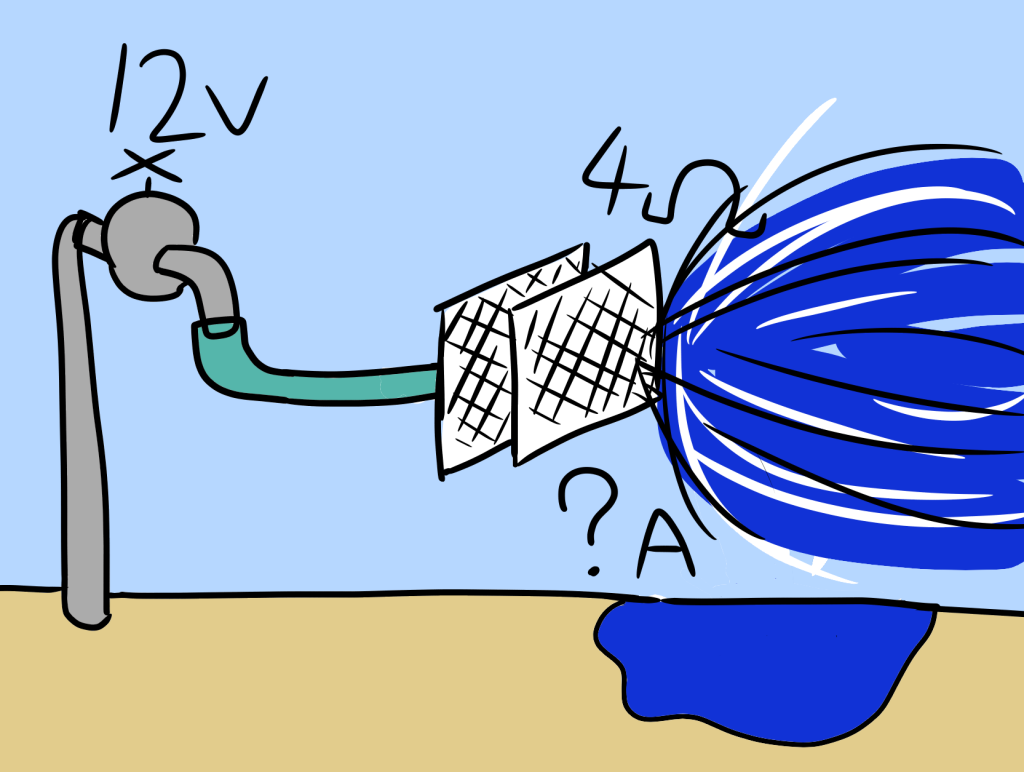
下記回路における電流値 I(A) を求めよ。
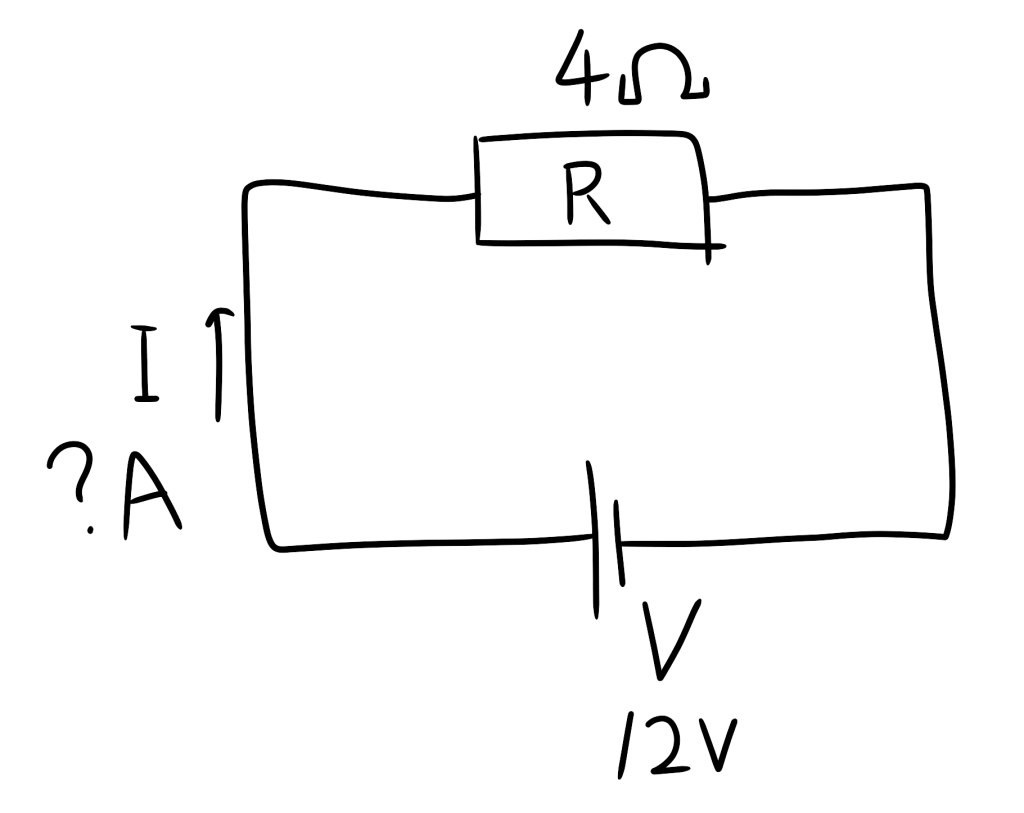
電圧:12V 電流:?A 抵抗:4Ω の回路です。
想像しにくいので、ちょっと形を変えてみます。
こうして…

こうですね。
すみません。こんがらがってきました。やめましょう。
とりあえず “電圧がスタート位置、電流と抵抗はセット” ということを覚えておきましょう。
電圧:12V 電流:?A 抵抗:4Ω です。式に当てはめます。
電圧 = 電流 x 抵抗
12 = ? x 4
この形になればもう大丈夫ですね。両辺を4で割って、
12 ÷ 4 = ? となりますので、3=?。
電流値は3Aとなります。
見直しに使えるホース理論
前項の計算で、12V = 3A x 4Ωとなりました。
果たしてこれがあっているのか?
実は、蛇口・水の勢い・フィルターを使うことで確認できます。
もし 電圧 = 電流 ÷ 抵抗 で計算してしまっていたらを考えてみましょう。
12 = ? ÷ 4 ※展開で途中式
12 x 4 = ? ÷ 4 x 4
12 x 4 = ?
? = 12 x 4
? = 48になります。
48 = 12 x 4
式だけ見ると問題ないですが、ここで抵抗値(フィルター)を増やしてみます。
フィルターを2枚重ねにすると計算式はこちらです。
96 = 12 x 8
フィルターを2枚に増やしたら、なぜか出てくる水の勢いが倍増しました。
明らかにおかしいですね。
まとめ
ひとまずこのくらいにしておきましょう。
無駄に遠回りしてしまった気もしますが、考え方としてはありかなと思っています。
蛇口 = 出口 x フィルター
電圧 = 電流 x 抵抗
これをしっかり覚えておきたい。
自分の中で想像しやすいものが見つかると覚えることも早くなりそうですね。
おわりに
最後まで閲覧いただき、ありがとうございます。
直列・並列や合成抵抗の話も何かの形で書いていきたいと思っておりますので、
もし見かけた際はよろしくお願いします。



コメント